Function Reflected Over X Axis

Reflect the graph of

$s\left(t\right)=\sqrt{t}\\$

(a) vertically and (b) horizontally.

a. Reflecting the graph vertically ways that each output value will be reflected over the horizontal t-axis every bit shown in Effigy 10.

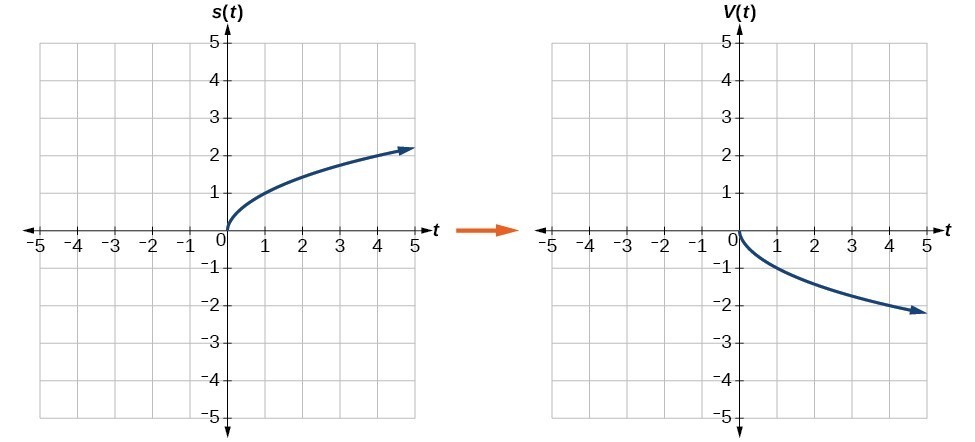Graph of the vertical reflection of the square root function. Figure 10.Vertical reflection of the foursquare root function

Considering each output value is the contrary of the original output value, nosotros tin can write

$5\left(t\right)=-due south\left(t\right)\text{ or }V\left(t\correct)=-\sqrt{t}\\$

Find that this is an outside change, or vertical shift, that affects the output

$s\left(t\correct)\\$

values, so the negative sign belongs outside of the role.

Reflecting horizontally means that each input value will be reflected over the vertical axis as shown in Effigy xi.

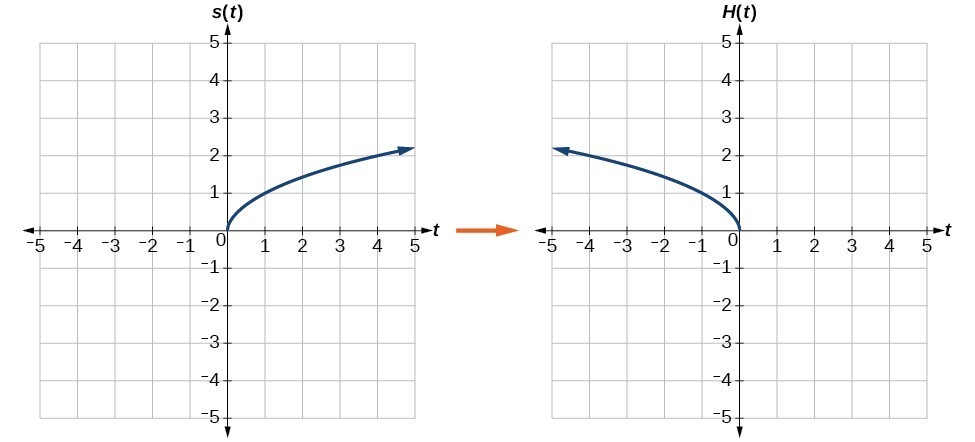Graph of the horizontal reflection of the square root function. Figure eleven. Horizontal reflection of the square root function

Because each input value is the opposite of the original input value, we can write

$H\left(t\correct)=s\left(-t\right)\text{ or }H\left(t\correct)=\sqrt{-t}\\$

Discover that this is an inside change or horizontal modify that affects the input values, so the negative sign is on the inside of the function.

Note that these transformations tin impact the domain and range of the functions. While the original foursquare root function has domain

$\left[0,\infty \right)\\$

and range

$\left[0,\infty \right)\\$

, the vertical reflection gives the

$5\left(t\right)\\$

function the range

$\left(-\infty ,0\right]\\$

and the horizontal reflection gives the

$H\left(t\right)\\$

function the domain

$\left(-\infty ,0\right]\\$

Function Reflected Over X Axis,

Source: https://www.coursehero.com/study-guides/tcc-fl-precalculus/graph-functions-using-reflections-about-the-x-axis-and-the-y-axis/