Length Of A Segment Formula

Eugene is a qualified command/instrumentation engineer Bsc (Eng) and has worked every bit a programmer of electronics & software for SCADA systems.

In this tutorial you'll larn about:

• names for different parts of a circle
• degrees and radians and how to convert betwixt them
• chords, arcs and secants
• sine and cosine
• how to work out the length of an arc and chord
• how to calculate the area of sectors and segments
• the equation of a circle in the Cartesian coordinate system

What Is a Circle?

"A locus is a curve or other effigy formed by all the points satisfying a particular equation."

A circle is a unmarried-sided shape, merely it tin can besides be described equally a locus of points where each betoken is equidistant (the same distance) from the middle.

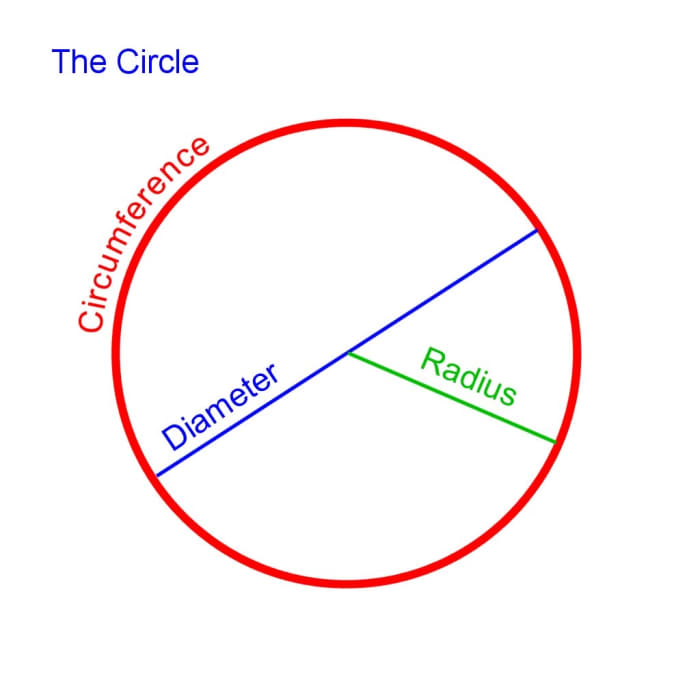
Circumference, diameter and radius

© Eugene Brennan

Bending Formed by Ii Rays Emanating From the Middle of a Circle

An angle is formed when two lines or rays that are joined together at their endpoints, diverge or spread apart. Angles range from 0 to 360 degrees. We frequently "borrow" messages from the Greek alphabet to use in math and science. Then for instance, nosotros use the Greek letter "p" which is π (pi) and pronounced "pie" to represent the ratio of the circumference of a circumvolve to the diameter. Nosotros also use the Greek letter θ (theta) and pronounced "the - ta", for representing angles.

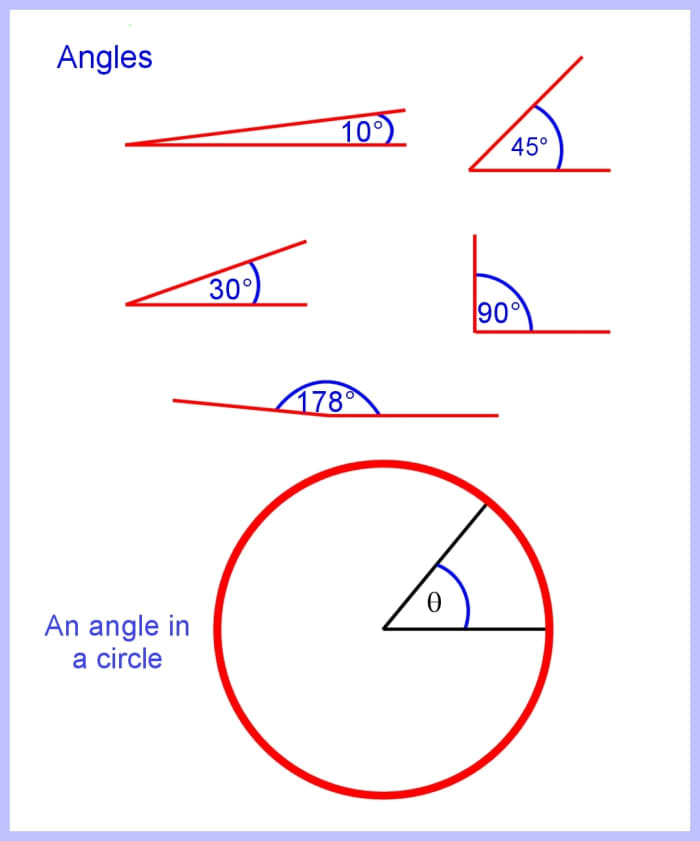
An angle is formed by 2 rays diverging from the heart of a circle. This angle ranges from 0 to 360 degrees

Paradigm © Eugene Brennan

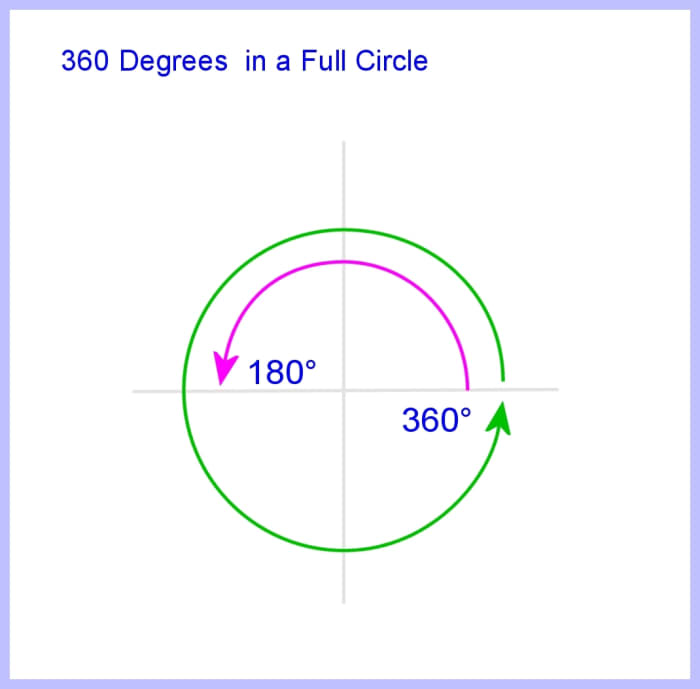
360 degrees in a full circumvolve

Image © Eugene Brennan

Parts of a Circle

• A sector is a portion of a round disk enclosed by ii rays and an arc.
• A segment is a portion of a circular disk enclosed past an arc and a chord.
• A semi-circle is a special example of a segment, formed when the chord equals the length of the diameter.

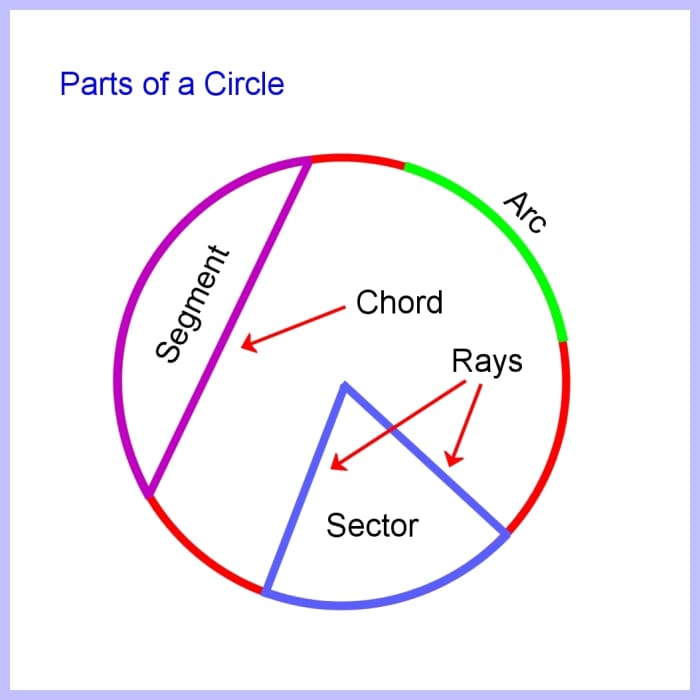
Arc, sector, segment, rays and chord

Paradigm © Eugene Brennan

What Is Pi (π) ?

Pi represented by the Greek letter π is the ratio of the circumference to the diameter of a circle. It's a non-rational number which means that it tin can't be expressed every bit a fraction in the form a/b where a and b are integers.

Pi is equal to 3.1416 rounded to four decimal places.

What's the Length of the Circumference of a Circle?

If the diameter of a circle is D and the radius is R.

So the circumference C = πD

Simply D = twoR

Scroll to Go along

Read More than From Owlcation

So in terms of the radius R

C = πD = 2πR

What'south the Area of a Circumvolve?

The area of a circumvolve is A = πR ^two

But R = D/ii

So the area in terms of the radius R is

A = πR ² = π (D/2)² = πD ⁱⁱ/4

What Are Degrees and Radians?

Angles are measured in degrees, just sometimes to make the mathematics simpler and elegant information technology's better to use radians which is another fashion of denoting an angle. A radian is the bending subtended by an arc of length equal to the radius of the circle. ( "Subtended" means produced by joining two lines from the terminate points of the arc to the middle).

An arc of length R where R is the radius of a circumvolve, corresponds to an angle of 1 radian.

So if the circumference of a circle is 2πR i.east 2π times R, the angle for a total circumvolve volition be 2π times 1 radian or 2π radians.

And 360 degrees = 2π radians.

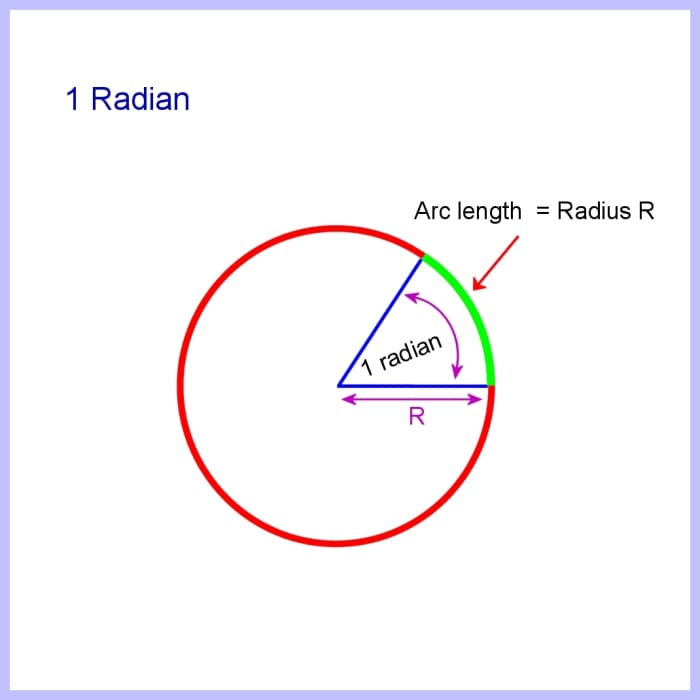
A radian is the bending subtended by an arc of length equal to the radius of a circumvolve.

Prototype © Eugene Brennan

How to Catechumen From Degrees to Radians

1. 360 degrees = 2π radians
2. Dividing both sides by 360 gives
3. 1 degree = 2π /360 radians
4. Then multiply both sides by θ
5. θ degrees = (2π/360) ten θ = θ(π/180) radians
6. So to catechumen from degrees to radians, multiply by π/180

How to Convert From Radians to Degrees

1. 2π radians = 360 degrees
2. Divide both sides past 2π giving
3. 1 radian = 360 / (2π) degrees
4. Multiply both sides by θ, so for an angle θ radians
5. θ radians = 360/(2π) 10 θ = (180/π)θ degrees
6. So to catechumen radians to degrees, multiply past 180/π

How to Find the Length of an Arc

Y'all can piece of work out the length of an arc by calculating what fraction the angle is of the 360 degrees for a total circle.

1. A full 360 degree angle has an associated arc length equal to the circumference C
2. And so 360 degrees corresponds to an arc length C = 2πR
3. Carve up by 360 to observe the arc length for one degree:
4. 1 degree corresponds to an arc length 2πR/360
5. To find the arc length for an angle θ, multiply the effect higher up past θ:
6. i x θ = θ corresponds to an arc length (2πR/360) ten θ

So arc length s for an bending θ is:

s = (2πR/360) x θ = πRθ /180

The derivation is much simpler for radians:

By definition, 1 radian corresponds to an arc length R

So if the angle is θ radians, multiplying by θ gives:

Arc length southward = R x θ = Rθ

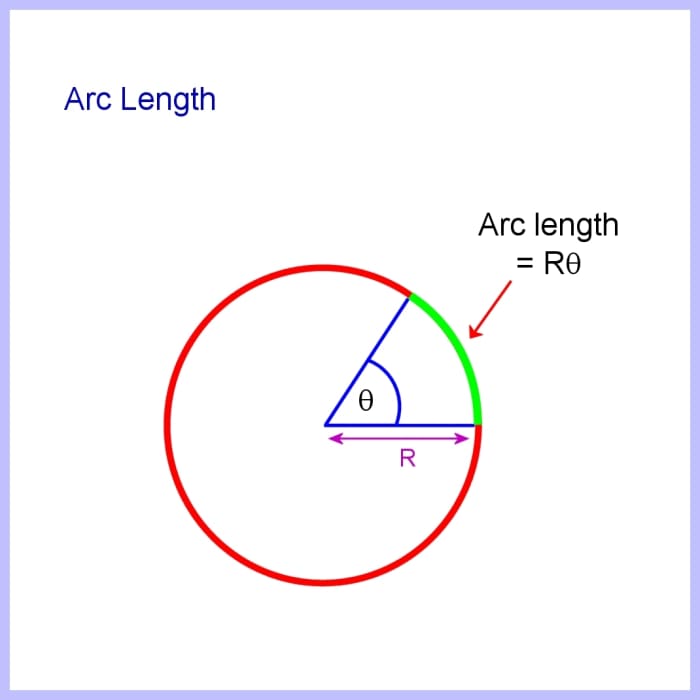
Arc length is Rθ when θ is in radians

Prototype © Eugene Brennan

What Are Sine and Cosine?

A correct-angled triangle has 1 angle measuring ninety degrees. The side opposite this angle is known as the hypotenuse and it is the longest side. Sine and cosine are trigonometric functions of an angle and are the ratios of the lengths of the other 2 sides to the hypotenuse of a correct-angled triangle.

In the diagram beneath, one of the angles is represented by the Greek alphabetic character θ.

The side a is known as the "contrary" side and side b is the "side by side" side to the angle θ.

sine θ = length of opposite side / length of hypotenuse

cosine θ = length of side by side side / length of hypotenuse

Sine and cosine apply to an angle, non necessarily an angle in a triangle, then it's possible to just have ii lines meeting at a point and to evaluate sine or cos for that angle. However sine and cos are derived from the sides of an imaginary right angled triangle superimposed on the lines. In the second diagram below, you can imagine a right angled triangle superimposed on the purple triangle, from which the opposite and adjacent sides and hypotenuse can be determined.

Over the range 0 to 90 degrees, sine ranges from 0 to 1 and cos ranges from ane to 0

Recollect sine and cosine only depend on the angle, not the size of the triangle. And so if the length a changes in the diagram below when the triangle changes in size, the hypotenuse c as well changes in size, but the ratio of a to c remains constant.

Sine and cosine are sometimes abbreviated to sin and cos.

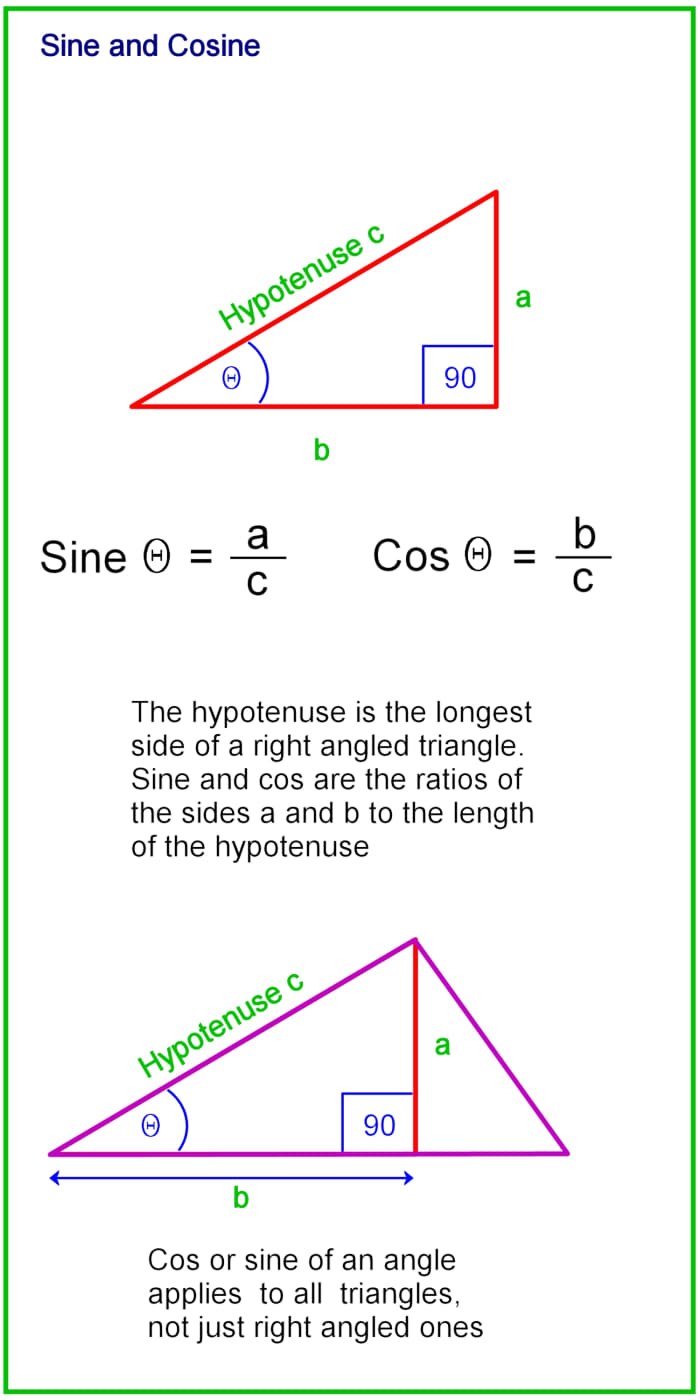
Sine and cosine of angles

Image © Eugene Brennan

How to Calculate the Area of a Sector of a Circumvolve

The total area of a circle is πR ^two corresponding to an angle of 2π radians for the full circle.

If the angle is θ, then this is θ/2π the fraction of the full angle for a circle.

And then the expanse of the sector is this fraction multiplied past the full expanse of the circle

or

(θ/2π) x (πR ^two) = θR ²/ii with θ in radians.

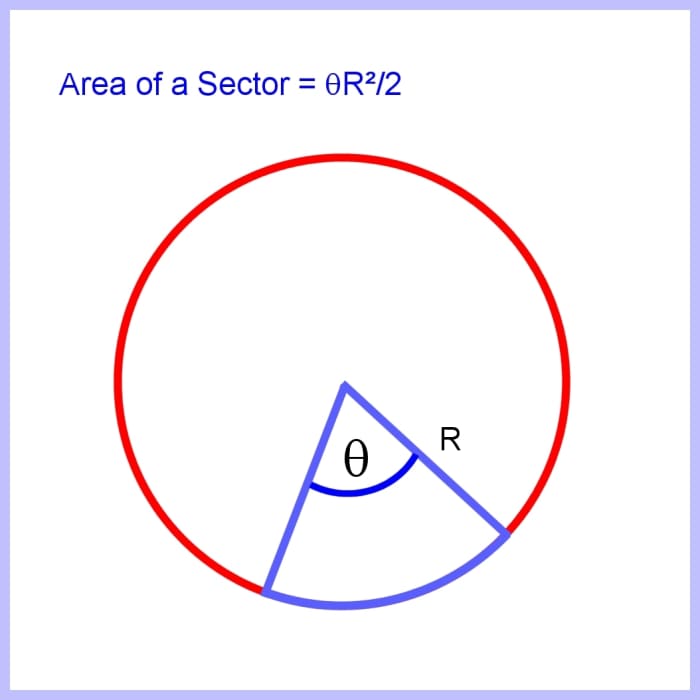
Expanse of a sector of a circle knowing the bending θ in radians

Prototype © Eugene Brennan

How to Calculate the Length of a Chord Produced by an Angle

The length of a chord can be calculated using the Cosine Rule.
For the triangle XYZ in the diagram beneath, the side opposite the angle θ is the chord with length c.

From the Cosine Rule:

c ² = R ² + R ² -iiRRcos θ

Simplifying:

c ^two = R ^two + R ² -2R ²cos θ

or c ² = iiR ² (one - cos θ)

But from the half-angle formula (i- cos θ)/ii = sin ² (θ/2) or (one- cos θ) = 2sin ^two (θ/2)

Substituting gives:

c^two = twoR ² (1 - cos θ) = 2R ²2sin ² (θ/ii) = ivR ²sin ² (θ/two)

Taking square roots of both sides gives:

c = twoRsin(θ/2) with θ in radians.

A simpler derivation arrived at by splitting the triangle XYZ into 2 equal triangles and using the sine human relationship betwixt the opposite and hypotenuse, is shown in the calculation of segment area below.

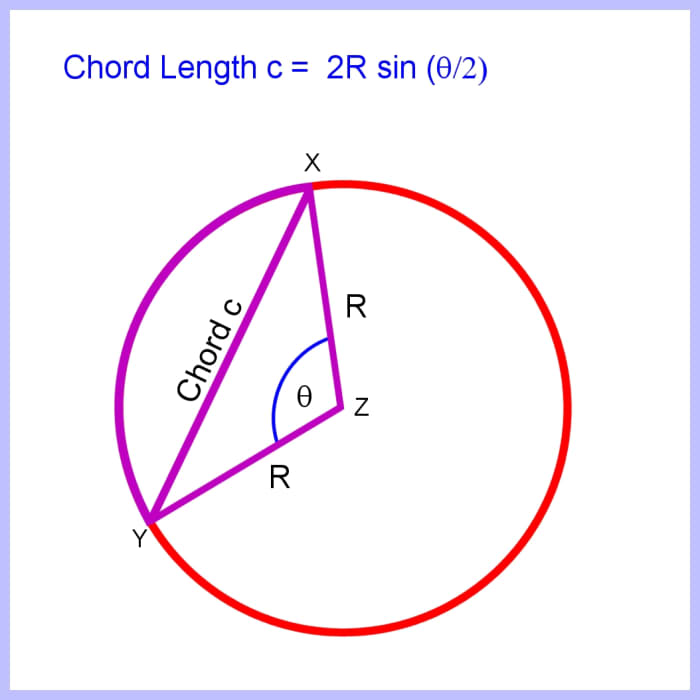
The length of a chord

Image © Eugene Brennan

How to Calculate the Area of a Segment of a Circle

To calculate the surface area of a segment bounded by a chord and arc subtended by an bending θ , first work out the area of the triangle, then subtract this from the area of the sector, giving the surface area of the segment. (meet diagrams below)

The triangle with bending θ can be bisected giving two right angled triangles with angles θ/2.

sin(θ/ii) = a/R

And so a = Rsin(θ/2) (cord length c = iia = 2Rsin(θ/two)

cos(θ/2) = b/R

And so b = Rcos(θ/2)

The area of the triangle XYZ is one-half the base past the perpendicular summit so if the base is the chord XY, half the base of operations is a and the perpendicular superlative is b. So the expanse is:

ab

Substituting for a and b gives:

Rsin(θ/ii)Rcos(θ/2)

= R ²sin(θ/2)cos(θ/ii)

Merely the double angle formula states that sin(2θ) = 2sin(θ)cos(θ)

Substituting gives:

Area of the triangle XYZ = R ^twosin(θ/2)cos(θ/2) = R ⁱⁱ ((1/2)sin θ) = (one/2)R ^twosin θ

Also, the area of the sector is:

R ²(θ/2)

And the surface area of the segment is the deviation between the expanse of the sector and the triangle, and then subtracting gives:

Area of segment = R ^two(θ/ii) - (1/2)R ²sin θ

= (R ²/two)( θ - sin θ ) with θ in radians.

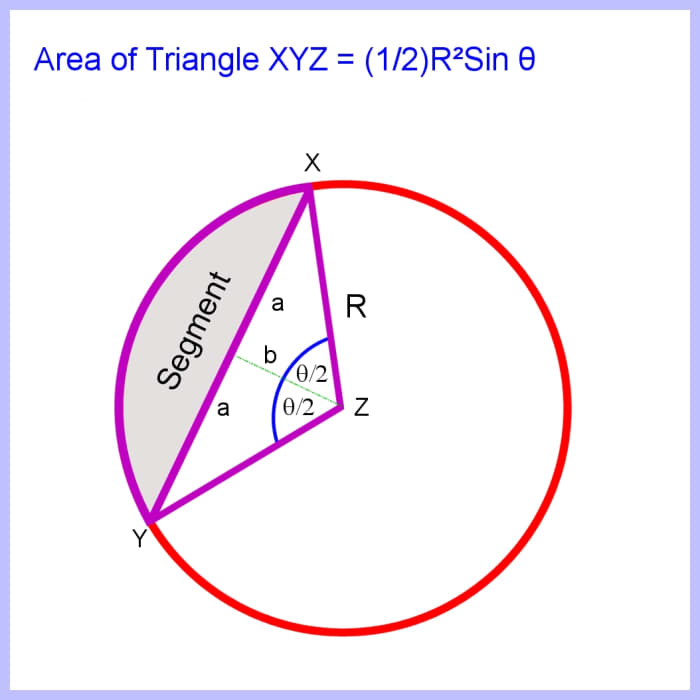
To summate the area of the segment, first calculate the area of the triangle XYZ and so subtract information technology from the sector.

Image © Eugene Brennan

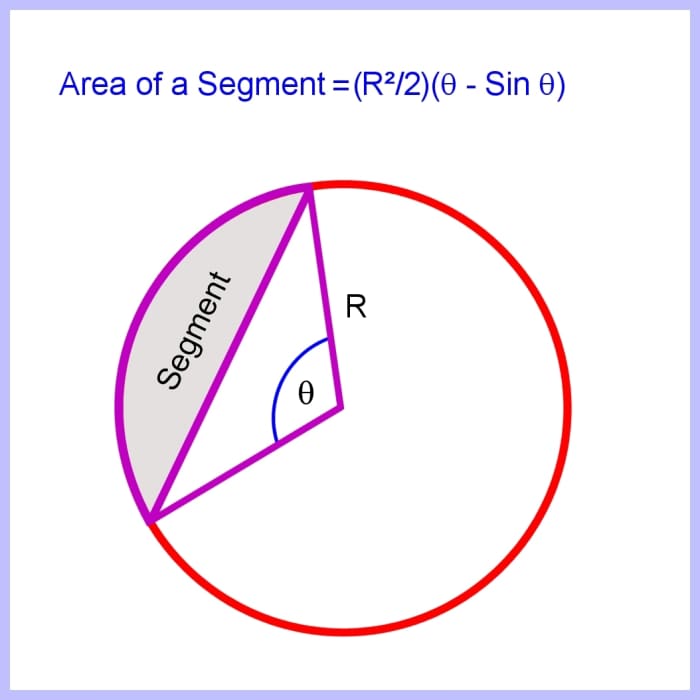
Expanse of a segment of a circle knowing the angle

Image © Eugene Brennan

Equation of a Circle in Standard Grade

If the centre of a circle is located at the origin, nosotros can take whatever betoken on the circumference and superimpose a right angled triangle with the hypotenuse joining this point to the center.
Then from Pythagoras's theorem, the square on the hypotenuse equals the sum of the squares on the other two sides. If the radius of a circle is r then this is the hypotenuse of the right angled triangle then we can write the equation as:

x ² + y ² = r ²

This is the equation of a circumvolve in standard grade in Cartesian coordinates.

If the circle is centred at the point (a,b), the equation of the circumvolve is:

(x - a)² + (y - b)² = r ²

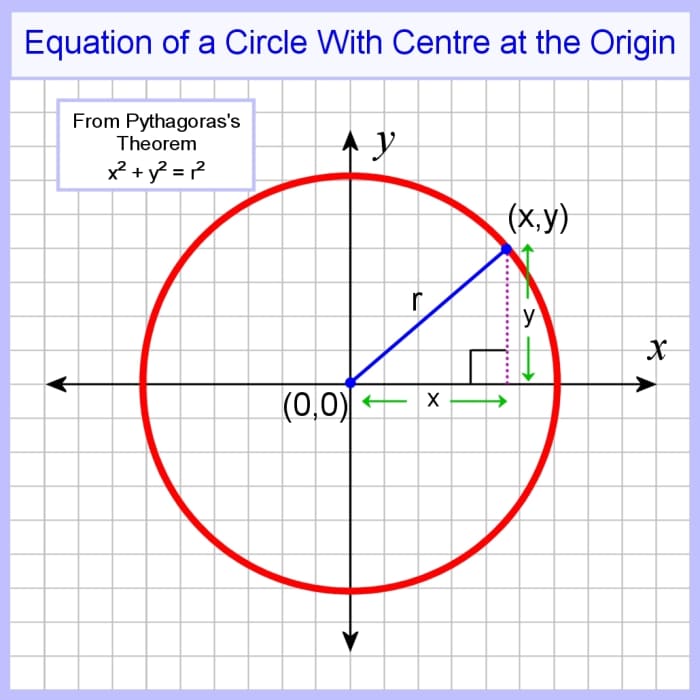
The equation of a circumvolve with a centre at the origin is r² = 10² + y²

Image © Eugene Brennan

Equation of a Circle in Parametric Class

Another fashion of representing the coordinates of a circle is in parametric form. This expresses the values for the 10 and y coordinates in terms of a parameter. The parameter is chosen as the angle between the x-axis and the line joining the point (x,y) to the origin. If this angle is θ, then:

x = cos θ

y = sin θ

for 0 < θ < 360°

Summary of Equations for a Circle

Circle formulas. θ is in radians.

Quantity	Equation
Circumference	πD
Expanse	πR²
Arc Length	Rθ
Chord Length	2Rsin(θ/2)
Sector Surface area	R²θ/2
Segment Area	(R²/2) (θ - sin(θ))
Perpendicular altitude from circle centre to chord	Rcos(θ/2)
Angle subtended past arc	arc length / (Rθ)
Angle subtended by chord	2arcsin(chord length / (2R))

Example

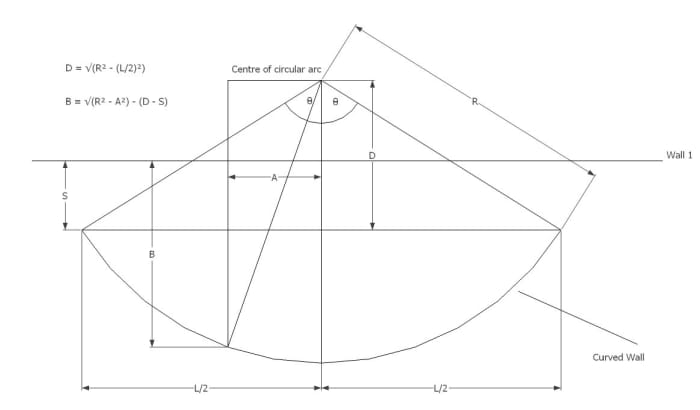
Here's a practical case of using trigonometry with arcs and chords. A curved wall is built in front end of a building. The wall is a department of a circle. It'due south necessary to work out the distance from points on the curve to the wall of the edifice (distance "B"), knowing the radius of curvature R, chord length L, distance from chord to wall Southward and distance from centre line to point on curve A. See if y'all can determine how the equations were derived. Hint: Use Pythagoras'due south Theorem.

This commodity is accurate and true to the best of the writer's knowledge. Content is for informational or entertainment purposes simply and does not substitute for personal counsel or professional advice in business organisation, financial, legal, or technical matters.

© 2018 Eugene Brennan

Eugene Brennan (writer) from Ireland on May 31, 2020:

Thank you Austen.

I worked out D in the diagram above knowing R and 50/2. In reality that's probably non necessary because you may already know the altitude from the eye of the arc to the within of the wall. Adding this to Due south gives you D.

Austen on May 31, 2020:

Many cheers for solving the curved wall event.

I' racked my brains back 45 plus used the existing formulae on your website to crack it- but as always when someone who "knows" tells you "how" - it becomes so articulate you wonder how y'all couldnt see it before.

Thanks for relighting the knowledge thirst.

A

Eugene Brennan (author) from Ireland on Apr 30, 2020:

Hullo Austen, I spent hours trying to effigy this out using angles, but it turned out that since the chord length is known between two ends of the curved wall (is this right?), information technology tin easily be worked out using Pythagoras'south Theorem. I've drawn it up every bit an example at the bottom of the article, promise it helps.

Suggestion, you could put the values into a spreadsheet to do the calculations.

Austen SMITH on Apr 28, 2020:

Hi I have a uncomplicated simply frustrating problem- I desire to build a regular curved wall a set distance from a straight wall - the centre of the circle /arc of the wall falls inside the building.

I need to work out distance from the direct wall to measure, at regular intervals, to create the perfect curve starting and ending on the chord (2d) forming the altitude from the straight wall.(1st chord)

Promise you can aid.

Eugene Brennan (author) from Ireland on April 07, 2020:

If yous hateful the chord length, it'southward 2Rsin(θ/2).

See the derivation above.

darrell on April 06, 2020:

how exercise i calculate the length of a segment of a circle

Lakshay on September 19, 2019:

Skilful efforts

Eugene Brennan (writer) from Ireland on April 05, 2019:

If you lot mean yous know the coordinates of the kickoff and end points of the chord, you can piece of work out the length of the chord using Pythagoras's theorem. Then utilize the equation for length of a chord (2Rsin(θ/2) to find θ.

Mazin G A on April 01, 2019:

Hi,

How can I calculate the angle at the middle of an arc knowing radius and center, starting time, and end points? I know how to do that if I take the length of the arc, but in my case I don't have it.

Eugene Brennan (writer) from Republic of ireland on March 19, 2019:

Thank you Troy, I'll keep information technology in mind. Parabolas will probably come first though.

Troy Sartain on March 19, 2019:

How most a similar commodity for ellipses? But a idea. Obviously, another level of complexity, even if not rotated.

Larry Rankin from Oklahoma on May 19, 2018:

Very educational.

Eugene Brennan (author) from Republic of ireland on May xviii, 2018:

Thank you George, I should have proof read before publishing, instead of beta testing on the readers !!

George Dimitriadis from Templestowe on May xviii, 2018:

Hi.

A good introduction to the basics of circle backdrop.

Diagrams are clear and informative.

But a couple of points.

You have And so C = πD = πR/two, which should be C = πD = 2πR

and A = πR^2 = π (D/2)two = πD^ii/2

should be A = πR^2 = π (D/2)2 = πD^2/iv

Length Of A Segment Formula,

Source: https://owlcation.com/stem/How-to-Calculate-the-Arc-Length-of-a-Circle-Segment-and-Sector-Area

Posted by: ochoascang1935.blogspot.com

Share this post